機械加工020　～真円度の測定、計算方法～

1. 真円度の定義とは

真円度の定義は上述した通りですが、理解できないですね。円筒状の部品の真円度が以下のように図面に記載されているとしましょう。
２次元の図面を３次元の図にしたもので考えると、、、

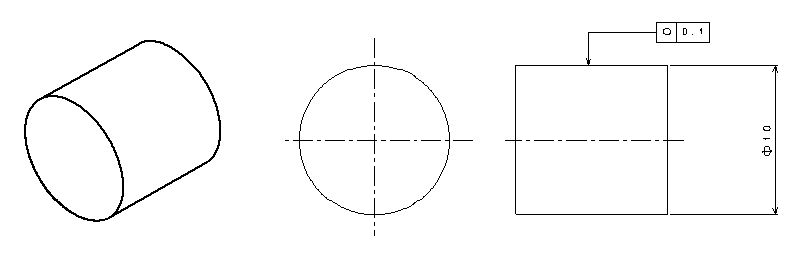
「軸直角断面における外周…」ですが、任意の適当な位置で軸方向とは直角に切断し、その断面を見てみましょう。この断面の外周が真円度を測定する部分です。
「え？どこを切断してもよいの？」
そうなんです。軸方向とは直角の輪切りの切断方向であれば、どこを切断(測定)してもよいです。

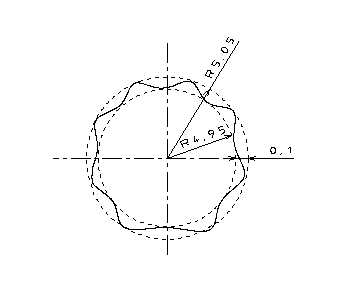
次に「…外周は半径の差が0.1mmの同心円の間になければ…」については図を見れば一目瞭然で、半径の差が0.1mm以下でなければならないという定義です。つまり真円度は半径で定義されているということがわかりますね。これは後述しますが、直径と勘違いしている人が多く、測定方法次第では合否判定を再計算する必要があります。

2.直径法(２点測定)と半径法 (３点測定)

真円度の測定方法は「直径寸法測定(直径法)」「凹凸(起伏)測定(半径法)」に大きく分けられます。それぞれメリットデメリットがあります。

2.1 寸法測定による真円度の評価

加工する立場であると、やはり寸法測定結果から判断できれば、作業は楽になります。基本的には内径でも外径でも同じなのですが、今回は上述した図面のように外径を例として挙げます。外径寸法はノギスやマイクロメータなどで測定できると思います。通常は円の任意1箇所を測定しますが、今回は90°ピッチで2か所(Ｘ方向とＹ方向)測定することとします。ここで注意しなければならないのは、真円度は同じ断面上で評価するためなるべく2か所の測定箇所の軸方向の違いが生じないようにします。この２か所の測定結果の差の１/２が「0.1以下」であれば、合格とできます。つまりこの方法は直径法なので、真円度の定義は半径法なのでそれに合わせる必要がありますね。

この方法であると簡単な測定器で真円度の検査をすることができますが、正確に真円度を評価していないため真円度の許容範囲が厳しい品物や、歪な形状の円には向いていません。以下の図でわかるように綺麗な楕円形状であればこの測定方法で正しく評価できますが、円が歪な形状であると測定する箇所によって測定値が安定しないため、2か所より多くの複数箇所を測定する必要があります。

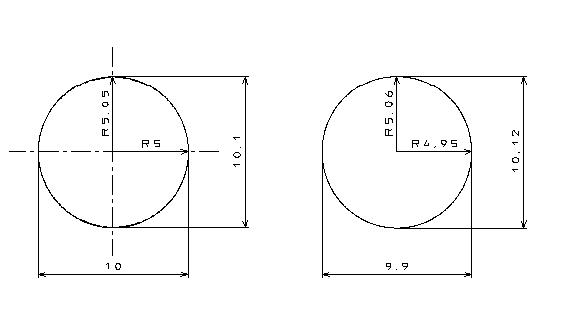
加工方法によっておにぎり(三角)形状になると、真円度が大きくても、寸法測定の結果は小さく評価され、ただしく判定できません。下図は真円度が0.48の三角形状の円です。これを2点測定で測定すると0.12となり、真円度が小さく測定されていることがわかると思います。

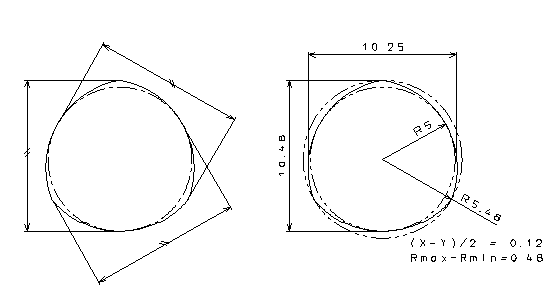
2.2　測定面の凹凸測定による真円度の評価

もうひとつの測定しては測定面の凹凸(振れ)を測定し、その最大最小差を半径差として評価する方法です。いろいろな測定機器がありますが、広く使用されているものは真円度測定機と言われるものです。この測定機はNC円テーブルに測定ワークを取り付け、テーブルと共にワークが回転し、測定子を測定面に接触させるもので、この時の測定ワークはワーク中心で回転します。測定結果は波形として表示されるため、どのような形状の円であるかは視覚的に認識することができ、複雑な形状であることが理由で測定値が小さいけど、実際の真円度が大きいものを見落とすことなどもありません。この方法であればどのような形状でも正確に高精度で測定が可能で、測定箇所を増やすことで真円度だけでなく、円筒度や直角度も併せて確認することができます。
ただし、この測定機は高額で、測定にも時間を要し、測定室などの温度管理された環境でなければ使用が困難です。そのため、場所を選ばず、安価で、素早く測定できるものとして挙げられるのが、３点式の測定方法です。これは90°や120°Ⅴブロックに測定ワークを載せ、ワーク頂点付近にダイヤルゲージやピックテスタなどの測定子を当て、ワーク1回転中の最大最小差(最大振れ量)を真円度と評価する方法です。
この方法は寸法測定での評価とは異なり、「振れ量＝半径差」なので「測定値＝真円度」とできます。しかし、この方法の測定値は「真円度測定機の測定値(真の値)」とは異なることがあり得ます。
真円ではない円の形状にはいくつもの凹凸があります。その凹凸面を基準に回転させるとワーク中心が上下することがわかります。もう少しわかりやすく理解できるように以下の図を見てください。

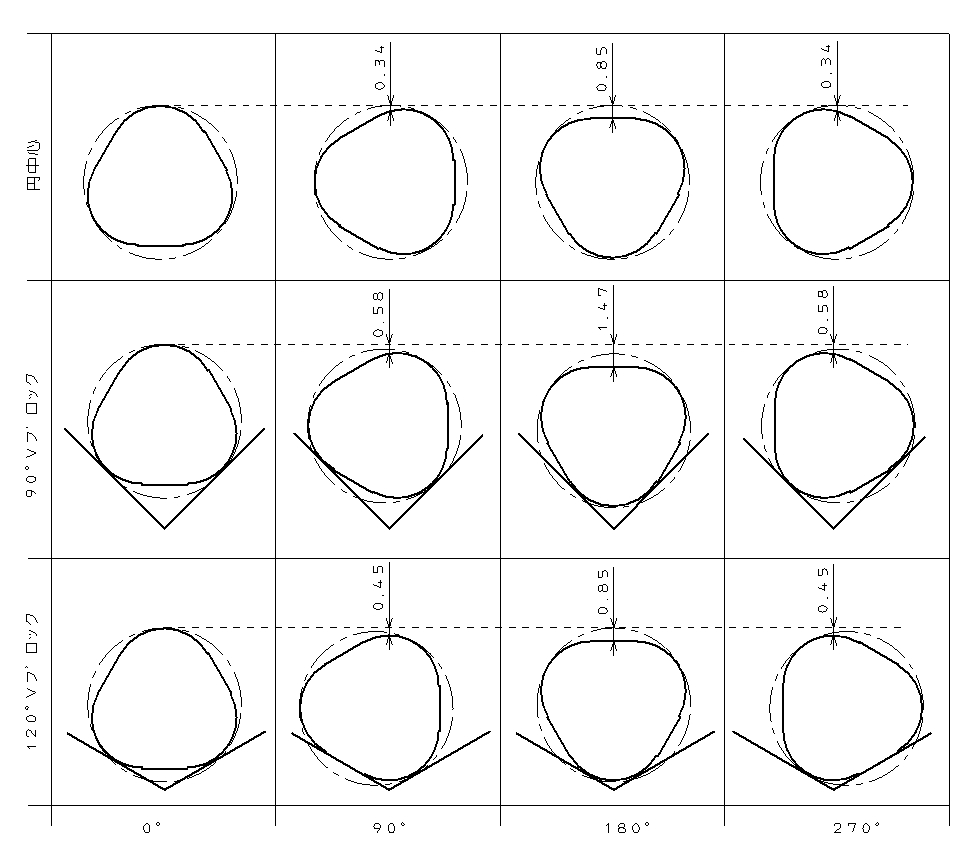
上記の図は三角形のおにぎり形状をした円を外径基準(３点法)の90°と120°Ｖブロック、円中心基準(真円度測定機)のそれぞれで測定した状態を表しています。90°ﾋﾟｯﾁで回転させた時の振れ(測定値)を比較すると同じ円(真円度)なのに、測定結果が違うのがわかります。
このように同じ形状の測定ワークであっても、Ⅴの角度によってワーク中心が上下する量が変わり、真の値(円中心で測定した値)とは異なる測定結果になってしまいます。また、同じＶ角度であっても円の角数ごともワーク中心が上下する量が変わってくるため、何角形の円形状であるかを予め把握していないと正しい測定結果を得る事ができません。

3. Ⅴブロック(３点測定)での真円度測定でもできるだけ正確な測定値を得るには？

まずは下の表を見てください。この表は円の角数とⅤ角度ごとで真の値(1)に対して、測定値が何倍になっているかを示しています。

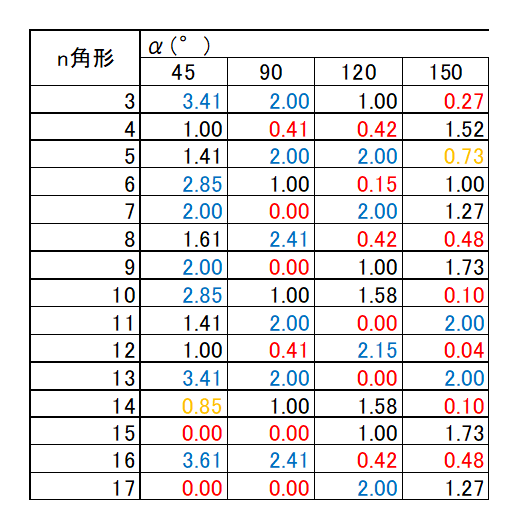
この表からわかるとおり、測定値が増幅するⅤ角度と減少するⅤ角度が円の角数で異なります。まずは起こり得る円の角数が予めわかっているなら、表からⅤ角度を決めることができますが、円の角数が分らない場合は有利な角数と不利な角数を打ち消し合うような2種類以上のⅤ角度で測定することで対策できます。例えば、45°で低倍の値となる場合、 120°は高倍の値となる角数が多いことからこのふたつのＶブロックで測定し、測定差が生じていないことを確認すれば、異常な真円度を見逃すことはないと思います。

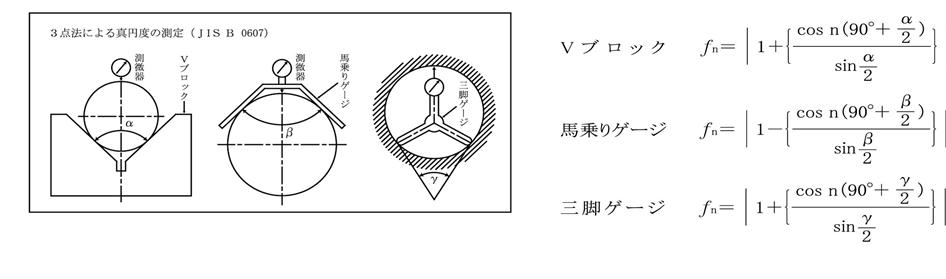
上記の表はJISで定められている計算式に当てはめたものです。あくまでも幾何学的に正確な形状であることが前提であるため、実際のワークは歪な形状の方が多いため、この理論値通りになることはほとんどありませんが、およその目安にはなり得ます。ただ、実際の加工現場では真円度のゼロをねらうことが多い為、段取りでは真円度測定機(円中心)で確認し、量産作業中は抜取りでＶブロック測定をすることが多いです。

4.まとめ

以上です。