
この部品とこの部品は取り付けることができるのに図面規格から外れているから不良品になるって合理的じゃないよね?

寸法の組合せによっては規格を広げてもOKっていう考え方があるよ。
機械加工の経験ある人にとってはあるあるなんですが、部品同士がくっつけば、機能的に満足するのに、無意味に図面規格が厳しいことってありますよね。
本来、部品同士が組立できれば目的を果たしているのに、図面規格を満足できないということだけで不良品になったり、特採として申請を挙げないとならないことがあり、生産スピードが低下します。そのため加工現場で機能的な問題が解決できると確認できれば、スムーズな生産が期待できそうです。この問題をすこし改善できる方法が最大実体公差という考え方です。あまり図面指示されていることが少ないですが、最大実体公差利用すれば不良品の改善ができそうです。
1.直角度の最大実体公差
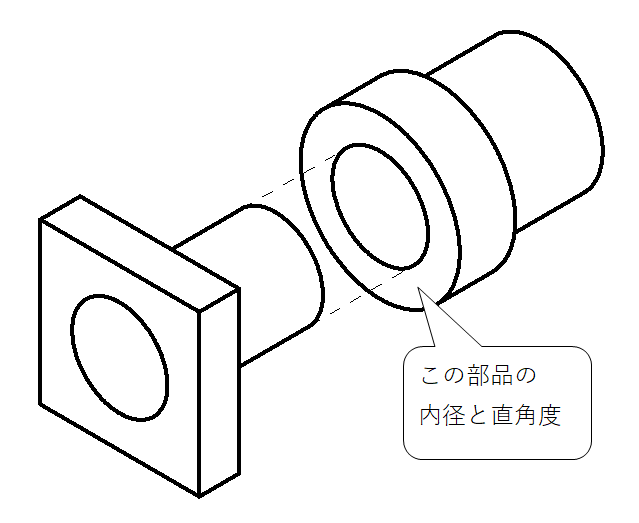
この部品は内径にピンを差し込むように使用するため、内径寸法に規格が設けられています。またピンはプレートに差し込まれているため、プレート接触面に対して、内径が傾いているとピンが奥まで入りきらず、部品同士が組立てできないことが考えられます。そのため、内径面にはプレート接触面(データムA)に直角度の規格が設けられ、下記のような図面で設計されました。
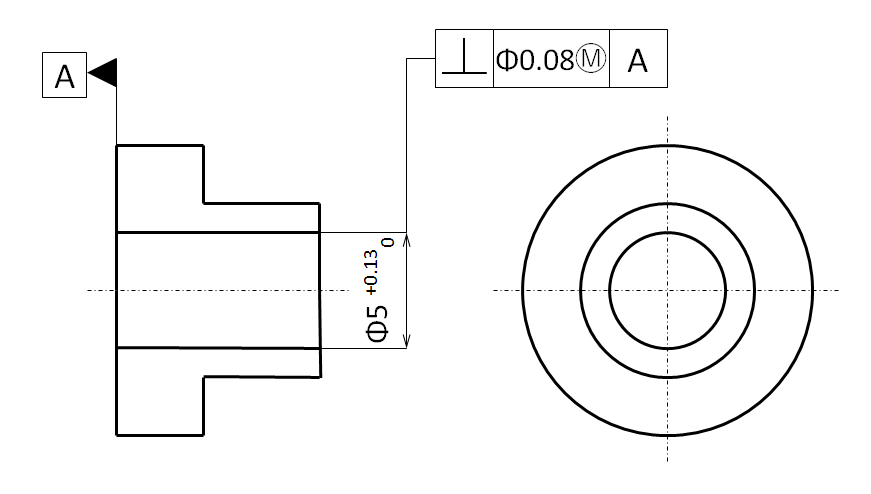
この図面には見慣れないⓂの表記がありますね。これが最大実体公差の記号で、これが追加されている直角度の規格Φ0.08は「内径寸法によっては0.08を超えてもよいですよ」って意味を表しています。
具体的に図で説明したいと思います。内径寸法はφ5 [0~+0.13]、直角度はΦ0.08 この寸法で最もピンが入れ難いのは「穴径が下限(マイナス)で直角度が最大」の時で、内径Φ50.00、直角度0.08です。
この状態を図で表すと以下の通りで、ピン径がφ4.92でも取り付けることができると言うことがわかりますね。
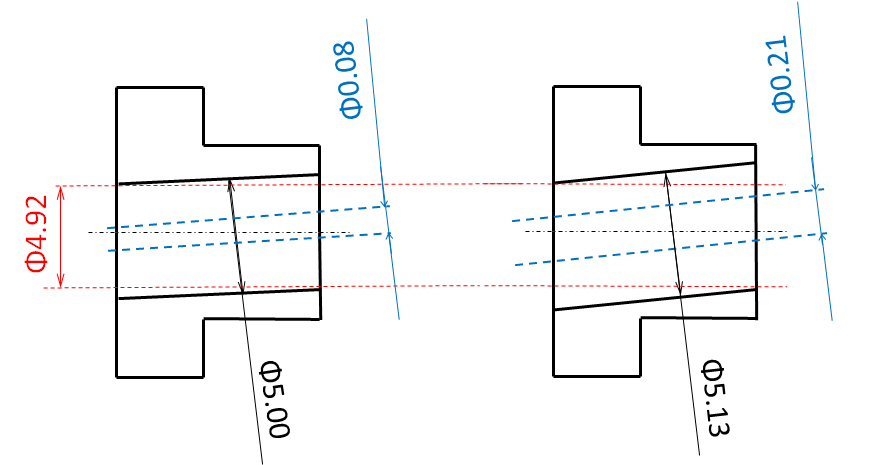
よってこの部品はφ4.92ピンを挿入することができれば、目的は達成しているという理解ができます。と言うことは、内径寸法が上限(プラス)であれば、Φ4.92のピンが挿入しやすいので、直角度は0.08でなくても良いと解釈できます。ではこれを計算するとΦ5.13-Φ4.92=Φ0.21となり、内径Φ5.13であれば直角度0.08ではなく、0.21まで合格としてよいということがわかります。
2.位置度の最大実体公差
最大実体公差でもっとも使用されている幾何公差は「位置度」です。位置度って何?ってわからない人は過去の記事で確認してください。

これも具体的な例で説明しましょう。
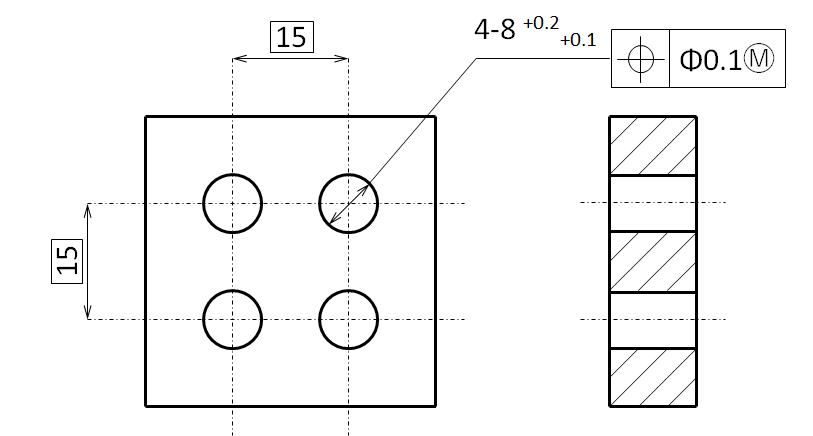
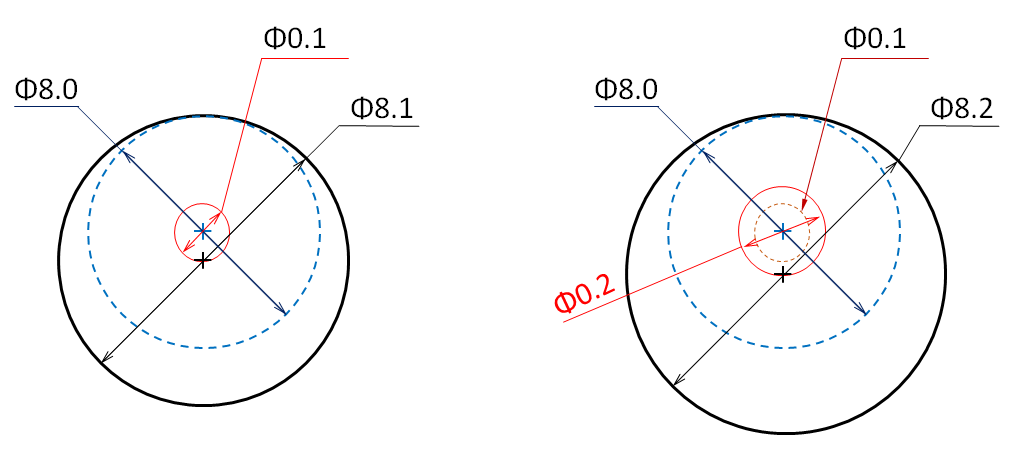
4-Φ8 [+0.1~+0.2]の穴径を位置度Φ0.1Ⓜで規格された図面があります。これも前述した例と似たように4つの穴に4本のピンが挿入できるような部品を想定してください。
これも同じように考えるとピンが最も入れ難い寸法の組合せは穴が小さくて位置度が最大の時で、Φ8.1、位置度0.1ですね。この時に挿入できる最大ピン径はφ8.0というのがわかります。そのためこの部品はΦ8.0ピンが挿入できれば目的は達成していることがわかります。では穴径が最大Φ8.2時に、Φ8.0ピンが挿入できるために必要な位置度はφ0.2ということになります。
以上






コメント