工程能力とは出来栄えのばらつき具合を数値化したものと以前の記事で紹介しましたね。おさらいですが、Cpは規格幅を6σ(シグマ)すなわち、6倍の標準偏差で割ることで求めることができます。このCpで工程能力が「ある」「ない」を判断することは間違っていないのですが、正確ではないです。それよりもCpkという値で判断することで、工程能力をより正確に判断することができます。Cpkをマスターすれば工程能力は理解したも同然。「Cpってなに?」って人はまずは以下の記事で復習しましょう。

1.偏りを含めないのはCp
まずは前回記事のおさらいをしましょう。σ(標準偏差)は以下の式でもとめられ、個々の値(データ)とそれらの平均値で成り立っています。

求めたい規格幅(上限値-下限値)を上記で求めた標準偏差×6で割ることでCpが算出できます。
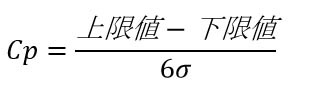
これによって求められた値は規格幅に対するばらつき(標準偏差)幅がどの程度であるかです。もう少しわかり易くすると、以下のようなデータを例にして説明します。
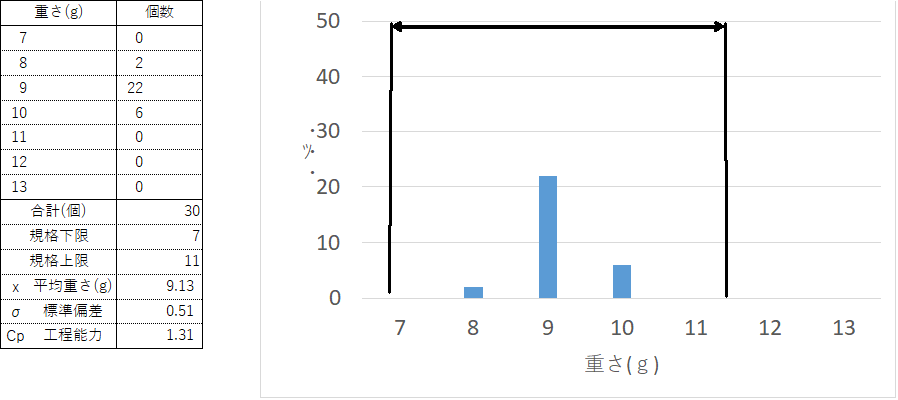
このデータの規格は上限値12、下限値8なので、規格幅は4ですね。単位は何でもよいですが、前回記事と合わせて「g(グラム)」とでもしておきましょう。そのため、求められたCpは「1.31」です。
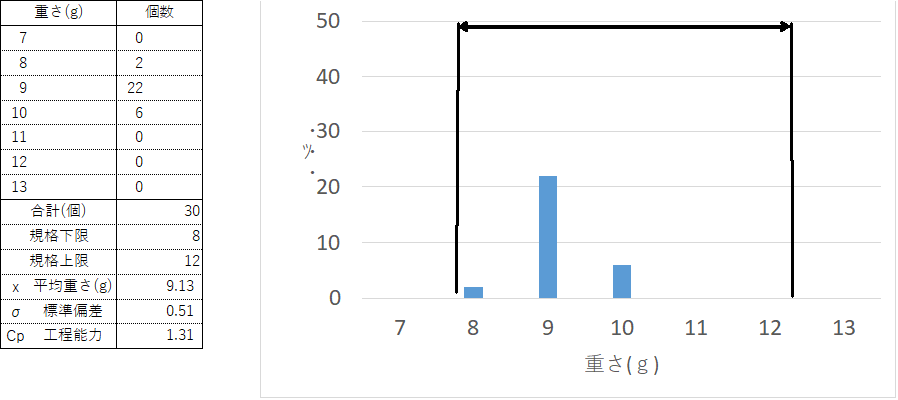
ここで規格を上限値11、下限値7に変更します。そうすると、前のデータは下限値ギリギリなので危なっかしい感じですが、変更後は規格中央にデータがバラついているので安心できますね。しかしこのふたつの規格は規格幅は同じ[4]なのでCpは「1.31」と同じです。そのためCpの計算では「規格幅に対するバラツキ度合い」を評価できますが、「バラツキが規格幅の偏り度合い」までは評価できません。この偏り具合を評価できるのが、Cpkになります。
2.Cpkを計算しよう。
では「どうやってCpkを計算するか?」ですが、計算は結構簡単です。

この計算式で求められた値に対して、小さい方をCpkとします。規格に対する偏りを「平均値~下限値」「平均値~上限値」として、それぞれ3σで割った値をCpkとします。3σにしているのは単純にCpは上下限値を6σで割っているのに対して、Cpkは平均値を基準にして上限、下限どちらかで算出するので3σとしています。また規格幅に対して厳しい値で評価すべきなのでどちらかの小さい値としています。これを先ほどの例として挙げたデータに当てはめてみましょう。
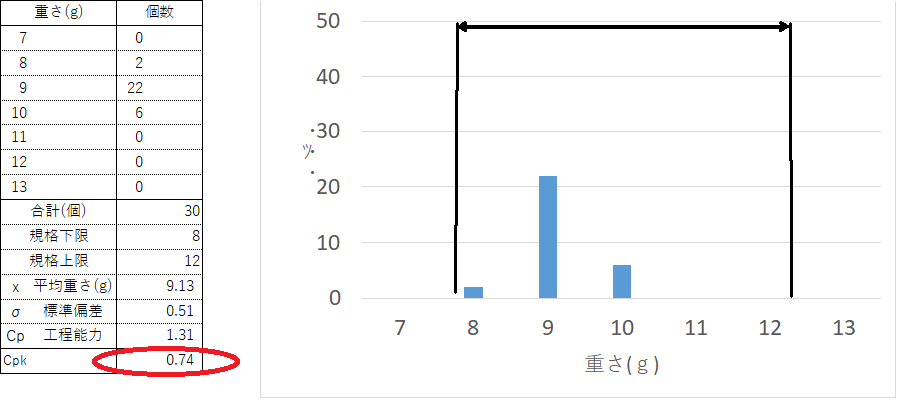
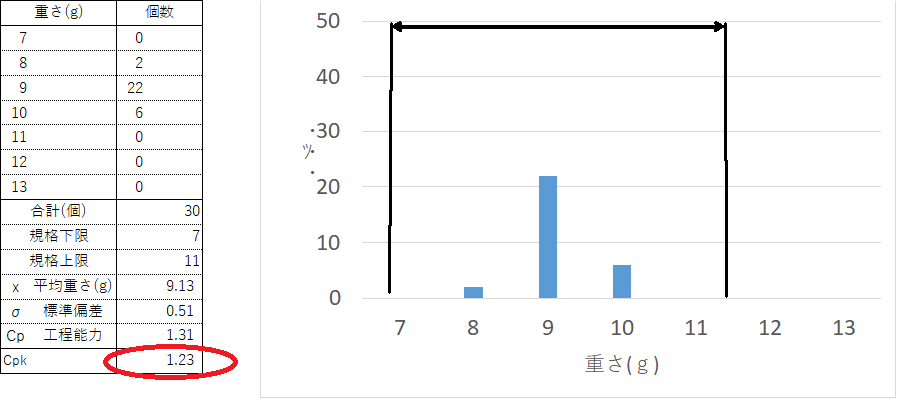
そうするとCp1.31と同じであったものが規格8~12gではCpk1.23 規格7~11gではCpk0.74であり値がだいぶかわりましたね。少し話が逸れますが、Cpkは以下の計算式でも算出することができます。これであればどちらか小さい方を選ぶ必要はありませんね。

3.片側規格
規格には両側規格と片側規格があります。前回の記事と同じように餃子の皮を例として説明します。今回計算した規格は8~12gといったように上下限に限界値が設定されています。このような両側規格のものを作る時、一般的には規格の中央を狙って作成します。つまり10gになるように狙って皮を作るのです。一方、餃子を包む時に皮の外周面に糊の役割として使用する水ですが、付け過ぎないようにある一定量以下でなければならないため、水はつけるけど、極力「0ml」になるように作業をするとおもいます。この場合、規格は2ml以下(2 max)となり、これが片側規格となります。片側規格のネライは常に規格限界値の反対側であり、ネライの偏りという概念がありません。そのため片側規格のCpとCpkは同じ値になります。
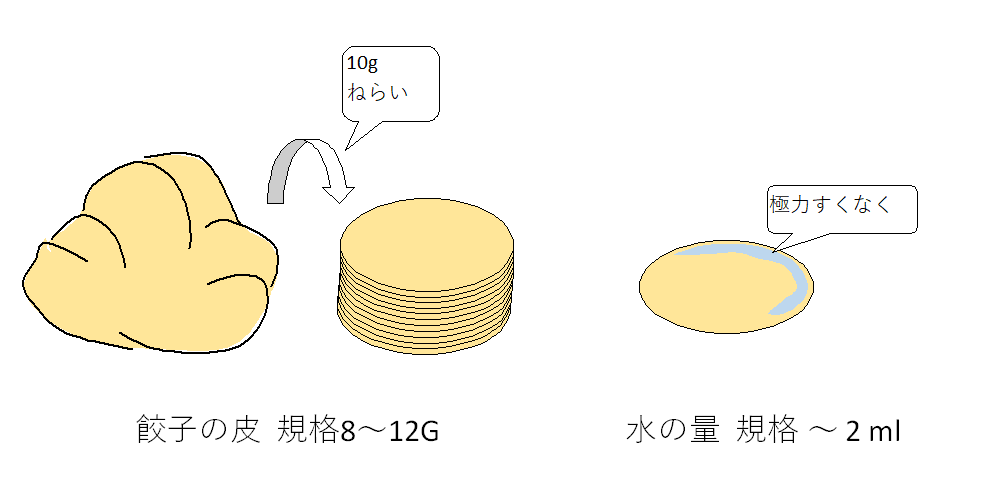
もう少し補足すると、両側規格はCpが良く(1.0以上)てCpkが悪い(1.0以下)とネライ(データの平均)を変更して、Cpkを改善することができます。前述のデータを例とすると、「改善前が平均9.13gであったので、10gを狙いにするため、いつもより1g多めに取る」といったようにできます。しかし、片側規格であるとネライは常に変わらないため、「水をつけない」以外、改善することができないためCpkという概念がなくなるんです。
では計算ですが、±3σを基準として値が大きい、小さいを評価するのが工程能力の考え方なので、両側規格は6σ、片側規格は3σで割ることになります。そうすると計算式は、、、上限規格と下限規格で計算式が異なりますが、考え方はCpkの計算と同じですね。

4.エクセルでの計算
参考にエクセルで計算することを想定して、これまでの計算結果を↓に載せておきます。
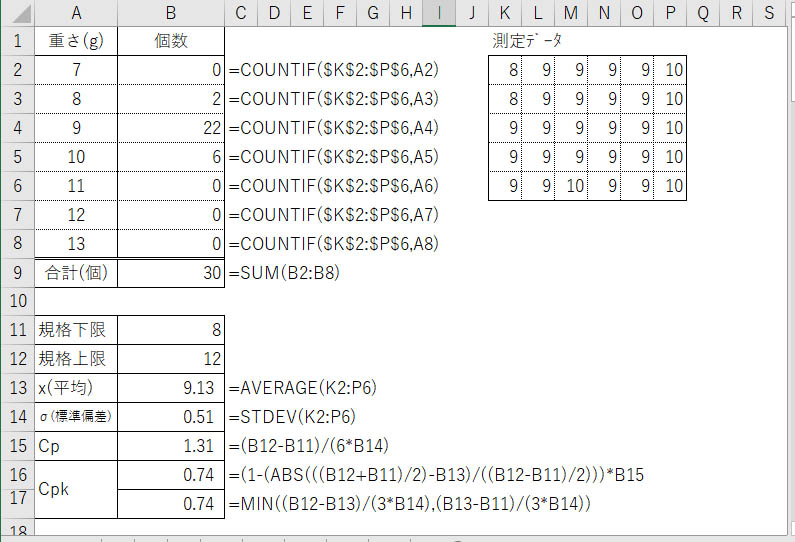
5.まとめ
・Cpはデータのバラツキを規格幅で評価してもので、規格に対する偏りは評価できていない。
・Cpkは規格に対する偏り具合を評価したもの
・両側規格は6σ、片側規格は3σをベースに工程能力を算出する。
・片側規格はネライの見直しができないため、Cpkという概念がない。
以上です。







コメント