工程能力とは

モノづくりをする上で規格というものがあります。
規格とは「主に産業や技術の分野において、製品や材料、あるいは工程などに関して定義された基準」
であるそうですが、わかりにくいですね。
ここで話をする規格というものは、重さ、長さ、量などの数値で管理できるものへの管理幅です。
管理幅なので、[100 ±1m]、[200 ±10 kg]、[50 ±2 ml]… などこんな感じです。
この規格(管理幅)に対して、モノの出来栄えがどのくらいの精度で出来上がっているかを数値で表現したものが工程能力です。
例えば、餃子の皮を作る場合、小麦粉をこね、皮1枚分の適量になるように同じ重さに分けます。同じ重さと言っても、やり方によっては重いものもあれば、軽いもののできてしまいます。皮が大きすぎると、最終的な餃子の大きさや味にも影響するため、ある範囲でその重さを管理したいですね。この「ある範囲の重さ」が規格であり、その規格に対して、重い、軽いがどのくらいバラツキがあるかを数値で判断できるように、計算したものが「工程能力」になります。
工程能力指数(CP)を使うとこんなことがわかる

上述した餃子の皮を例とすると、大きな小麦粉の塊から、人間が同じ重さになるようにひとつずつ、目分量で取り分けます。目分量と言っても、同じ重さになるように目指すべきだいたいの重さになるように作業をすると思います。たとえば、8~12gの範囲の重さで作ると最終的な餃子の出来栄えに差が生じなくなるとすると、当然8~12gの中央である10gを目指して取り分けます。
しかし、目分量であるため、10gのものもあれば11gや12g、まれに13gといったように規格から外れるものもできます。このバラツキ具合が良い状態か?悪い状態か?を判断するには膨大なデータを取り続ける必要があります。
下のグラフはヒストグラムとよばれるもので、餃子の皮の重さを計測し、同じ重さが何個あったかを
グラフにしたものです。さらに同じ過程で作られた皮をランダムで30個、300個それぞれ抜き取って重さを測定しました。
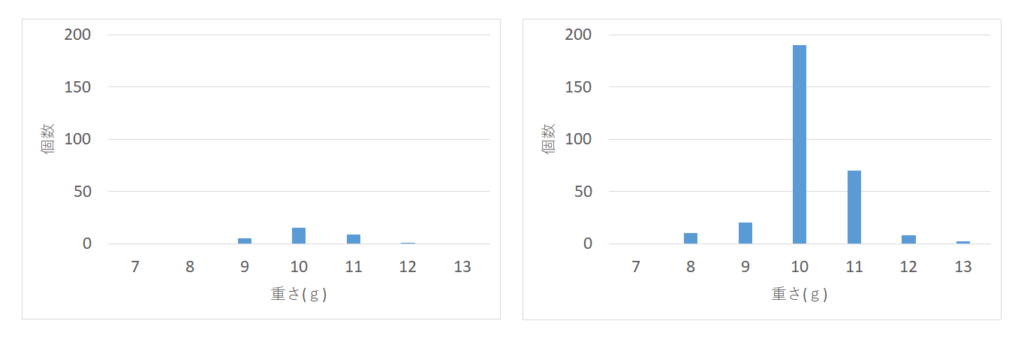
右図は300個のデータ、左図は30個のデータのグラフで、どちらも同じような形になっていますが、データの信頼性は測定数が多い右図の方が明らかです。
左図は30個しか測定していないので規格から外れるものが発生するかはよくわからないですが、右図の300個を見ると規格外れ(13g)が数個発見されていますね。
これらは同じ過程で作られた餃子の皮を任意に30個、300個抜き取り測定したデータなので、どちらも同じようなバラツキ具合になるはずですが、やはり30個データだけでは規格外れが発生するのか判断できないですね。しかし工程能力指数を計算すると左図のような少ないデータからでも、どれくらいの発生率で規格から外れるものがあるかを数値で予測することができます。
標準偏差とはなんですか?
「さあ、工程能力指数の計算方法をはやく教えて!」ですが少し待ってください。
まず、その前に標準偏差というものを知る必要があります。標準偏差とは、平均値から見たばらつき具合を数値化したものです。
「ん?Cpとの違いがわからん!」
Cpは規格幅に対してバラツキ具合を数値化したもので、標準偏差は規格とは無関係で平均値から見たバラツキ具合ですので、標準偏差には「規格」という概念がありません。
式で表すと↓の通りです。
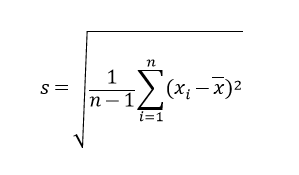
「あー無理、意味わかんない」ですよね。
では少し簡単にするとこんな感じです。
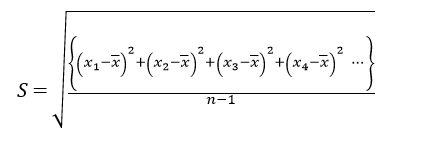
すこしはわかりましたか?平均値との差を2乗して、全部足して個数で割って、√(平方根)で計算。
すこし、わかるように例を記します。
10点満点のテストの5人分の点数に2点 4点 7点 8点 9点であったことを例にあてはめると、、、
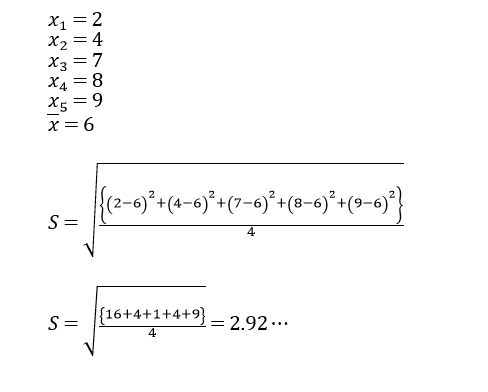
こんな感じです。
「と言われても、まだわかんない。」
安心してください。PCがあれば、エクセルで簡単に計算できます。
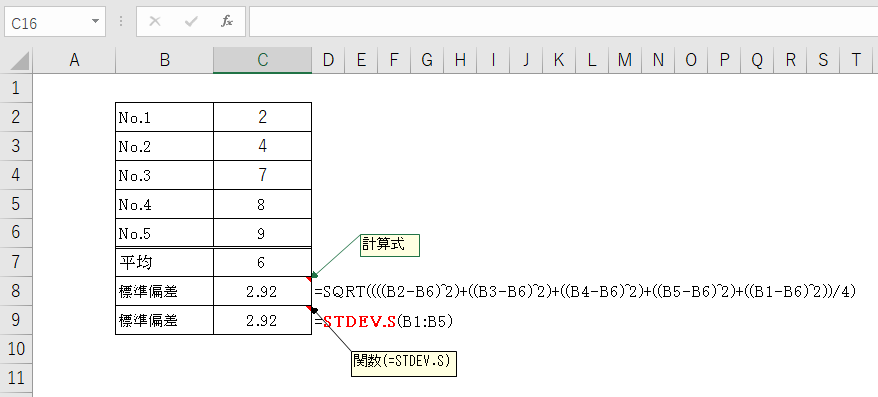
どうですか?セルに関数(STDEV.S)を入力するだけなので、上の計算式はさっぱり忘れてくれて問題ありません。ただし「標準偏差は平均のバラツキ」は覚えてくださいね。
工程能力指数(Cp)を計算しよう
Cpは以下のような計算式で求めることができます。

すこしややこしいのですが、σ は標準偏差を表しています。(上述したSですね。)
ここで理解しなければならないのは「6σ(±3σ)は99.7%が規格内であり、0.3%が規格外となる」です。
下図はある規格の中央値を起点に左右均等にバラツキが生じたと仮定した時の±σ、±2σ、±3σの標準偏差ごとでのバラツキが分布の何%であるかを示したものです。
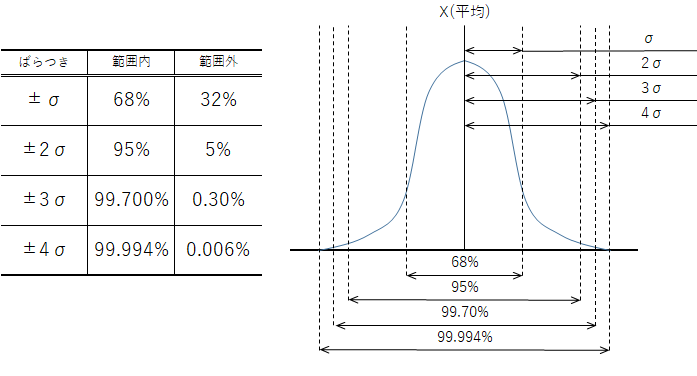
この図を基に考えると、Cpは1を基準に考えることが多いです。
[UTL – LTL = 6σ]であるとすると、計算式上は[Cp = 6σ/6σ = 1]となり、規格幅が6σであると、99.7%が規格内であることがわかります。
また[UTL – LTL = 8σ]であるとすると、計算式上は[Cp = 8σ/6σ = 1.33]となり、規格幅が8σであると、99.994%が規格内であることがわかります。
つまり、Cp=1以上あると規格外が0.3%の確立で発生し、Cp=1.33以上であれば0.006%の確立でしか発生しないんですね。
まとめ
・工程能力(Cp)とは規格幅に対するバラツキ具合を数値で判断できる計算手法である ・Cpを計算することで少ない個数のデータから、おおよそのばらつきを知り、何%が規格内であるかを予測できる。 ・標準偏差は平均値とのバラツキ具合を数値化したもの ・Cp=1.00では99.7%、Cp=1.33では99.994%が規格内である。
工程能力Cpが1.33以上あれば、良い状態とか、Cpが1.0以下は悪い状態とか聞くことがありませんか?
これは単純に不良発生確率の問題であって、不良が発生しないのではないです。
一般的な各Cpに対する検査頻度の考え方は以下の通りです。
CP ~1.00 全数検査
CP 1.00~1.33 抜取検査
CP 1.33~ 検査なしと判断しても良いレベル
餃子の例を挙げると、Cpは0.88でしたので最適なおいしさを保証するのであれば、皮を全数計量しなければならないですね。これが面倒であれば、規格幅を[8~12g]を[7~13g]に変更すればCpが1.32となるので、そこそこのおいしさは保てることができそうですね。ちなみにCp以外にもCpkというものがあります。この説明は長くなりそうなので次回、紹介します。

以上です。







コメント