1.真直度の定義
真直度は「JIS B 0621」では 「真直度とは直線形体の幾何学的に正しい直線からの狙いの大きさをいう。」としています。
って言われても、わからないですね。簡単に言うと、どれだけ真っすぐか?の度合いを表したものですが、厳密に言うと3種類の真直度があります。言葉だけでは理解しにくいですが、それぞれに図があるとわかりやすいです。
1.1 一方向の真直度
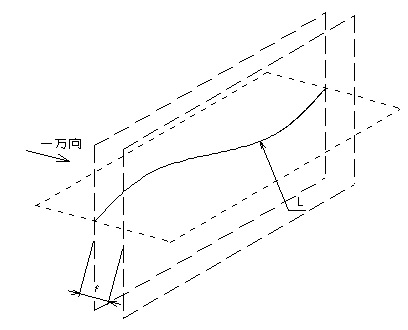
ある方向に垂直な幾何学的に正しい平行な二平面でその直線形体(L)を挟んだとき、平行二平面の間隔が最小となる場合の二平面の間隔(f)で表す。
1.2 互いに直角な二方向の真直度
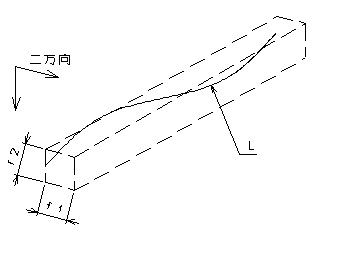
互いに直角なの水平および垂直方向の真直度は、その二方向にそれぞれ垂直な二組の幾何学的平行二平面でその直線形体(L)を挟んだ時の二組の平行二平面の各々の間隔が最小となる場合の二平面の間隔(f1 f2)で表す。
1.3 方向を定めない真直度
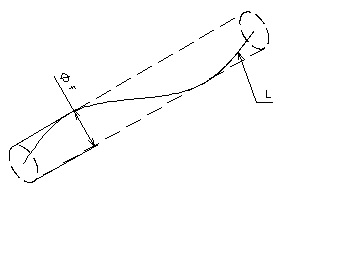
方向を定めない真直度はその直線形体(L)をすべて含む幾何学的円筒のうち、最も径の小さい円筒の直径(f)で表す。
2.真直度の図面への指示の仕方(φなし、φありの違い)
2.1 平面形状の真直度(φなし)
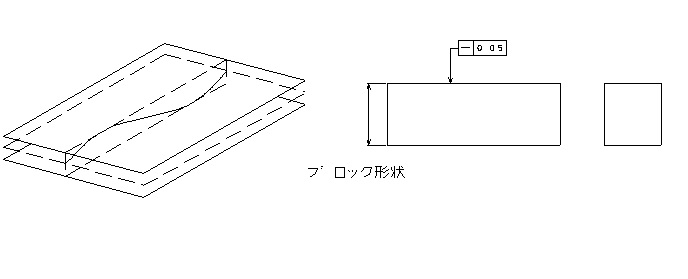
一般的でわかりやすい指示としては「一方向の真直度」で、代表的なものとしては立方体のブロック形状が挙げられます。図面指示としては、真直度が必要な面に、幾何公差を示します。
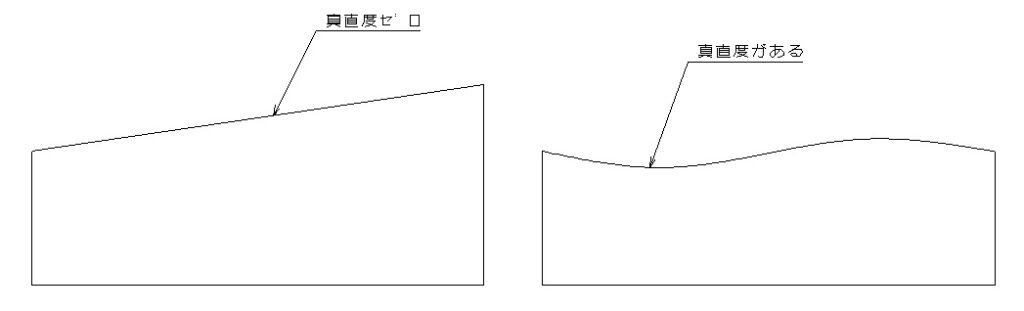
真直度は指定面がどれだけ真っすぐか?をしめしたものなので、基準面(データム)の指定はしません。上図のように一定範囲内に、真直度は最大最小の凹凸の差で評価するために、ある面に対して傾いていても指定面が真っすぐであれば真直度はゼロで、逆にどれだけある面に対して平行であっても凹凸があれば真直度はあると考えます。
ちなみに真直度の指定面は図面の指示方向で評価する軸方向を決めています。そのため指定面全域の真直度が必要と考えるのであれば、それは平面度になります。平面度については後日、記事にしたいと思います。
2.2 円筒形状の真直度(φなしφありのちがい)
円筒形状の真直度の指示は以下のようにφありとφなしで大別されます。
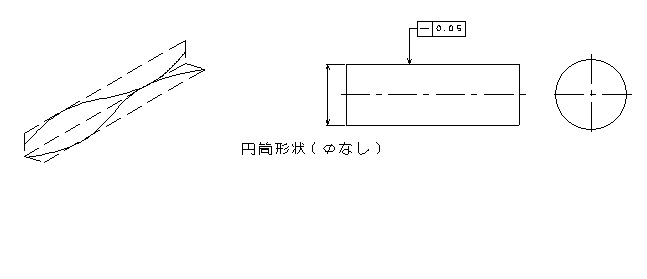
φなしの指示であると円周上360°どこでも凹凸量が規制されますが、測定する箇所(線)はそれぞれ独立して評価されます。つまり円周上、複数個所測定し、それぞれの測定値の凹凸量が最も大きな値で判断されます。
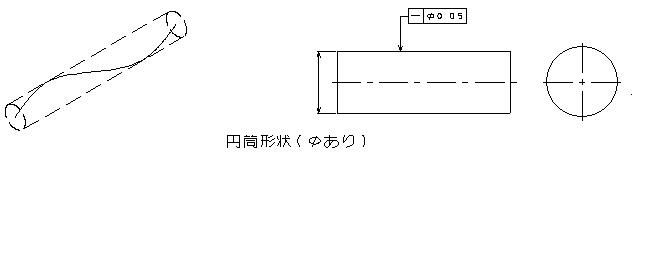
一方、φありの場合は図からもわかるように、一定空間内の円筒内に母線(評価面軸芯)が収まっていることで判断しています。そのため、Φなしと違い、測定する箇所はそれぞれ独立している訳ではなく、相関性を持って判断されます。
3.真直度のさまざまな測定方法
3.1 単純な面の真直度の測定
真直度の測定の仕方として、一般的なのはダイヤルゲージなどでブロックの上面を一方向に複数測定し、最大最小差で判断します。ですが、実際にはこの測定は平行度を測定しているに過ぎません。前述したように真直度は平行度とは違うので、この測定値をそのまま真直度として判断することはできません。そのため、複数の測定値に対して、計算をしなければなりません。
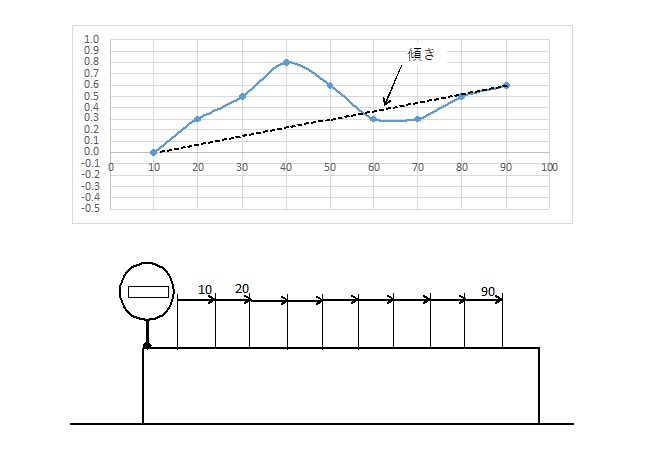
まず説明がしやすいように、測定位置をX軸、測定値(凹凸量)をY座標のグラフとします。この状態であるとブロックが傾いている度合いで測定値が際限なく大きくなりますので、この傾きをキャンセルします。キャンセルの仕方はいろいろありますが、今回はわかりやすいように「y=ax+b」としてプロットデータを2次関数にします。
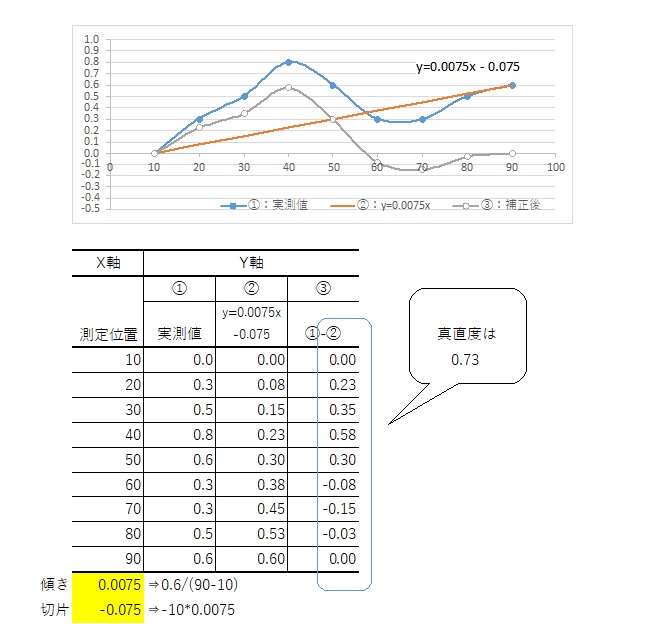
関数にするためには適当な2点が必要ですが、できればブロックの端から端付近のプロットデータを選択しましょう。計算方法としては両端のプロットデータ{x=10,y=0.0} {x=90,y=0.6}を「y=ax+b」に代入して求めます。この2点から計算された式は「y=0.0075x-0.075」となります。この式により各測定値(x)でのyの値を求めると、②になり、この②と①(実測値)との差が傾きをキャンセルした値(③ y)となります。この③の最大最小差が傾きをキャンセルした真直度となります。
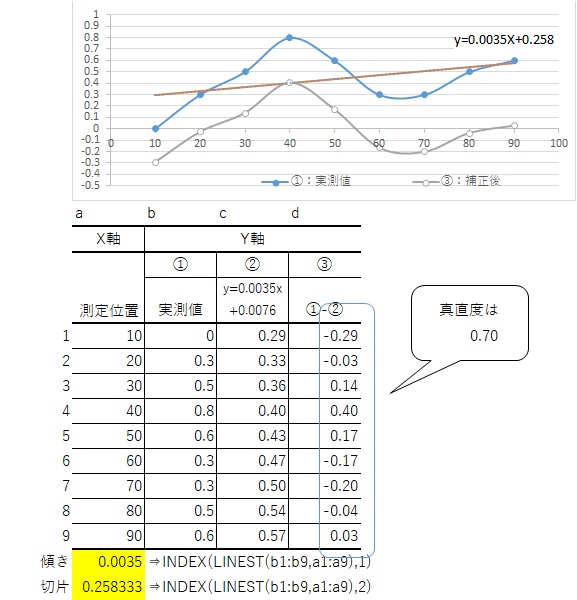
この方法は説明しやすいように始めのプロットと終りのプロットから2次関数式を求めましたが、実際の漸近線は少し傾きが小さいので少し違いますね。これを厳密に計算するためには最小二乗法と言う小難しい計算が必要です。しかしEXCELのLINEST関数を使用すれば難しい計算は不要です。
【最小二乗法によるexcelでの関数の計算方法】
y=ax+b
a(傾き)=INDEX(LINEST(yの値,xの値,),1)
b(切片)=INDEX(LINEST(yの値,xの値,),2)
3.2 円筒形状の測定
「3.1」で説明したように真直度は傾きをキャンセルした値で評価しなければならないことは理解できましたね。実際の平面形状では任意の一軸線上を複数プロットしますが、円筒形状はそうではなく、φありとΦなしで測定方法も変わります。
φなしの場合
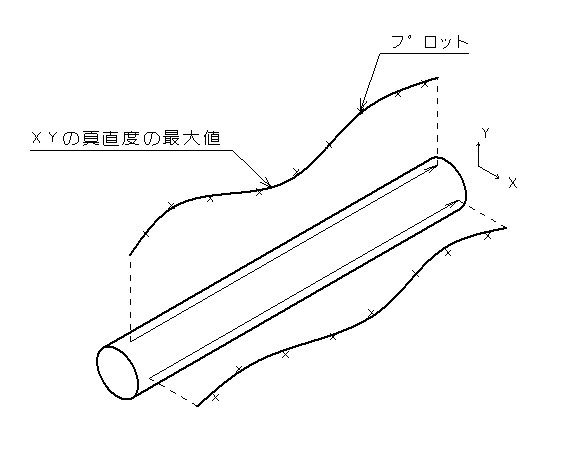
図のように回転方向に複数の一軸線上を複数プロットします。上述したように傾きをキャンセルした複数プロットデータの最大最小差を求めます。それぞれの複数の一軸線上の最大最小差からさらに最大なものが真直度になります。なお、回転方向に複数の軸線上の測定をすればするほど、高精度に評価ができますが、それでは効率が悪いです。そのため回転方向、90°間隔に2軸(XY)測定のが一般的で、加工で真直度が大きくなる場合の大半は反りや曲りによるものです。そのためXY軸を測定すれば真直度の最大値はおおよそわかるということが前提となります。
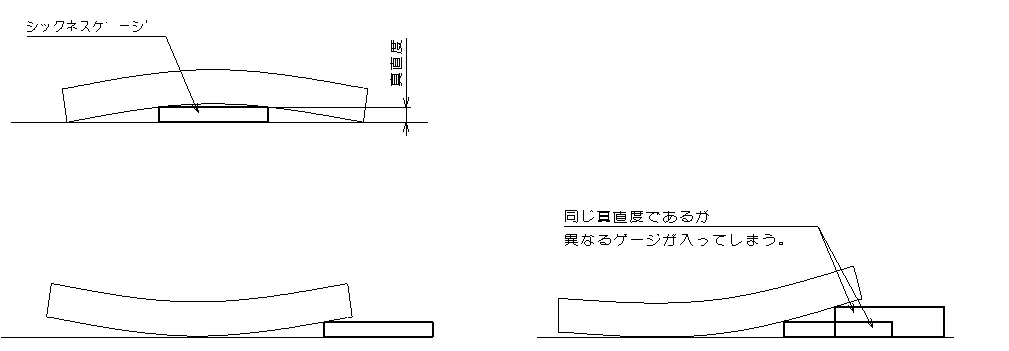
またワークを定盤において、XY軸方向をそれぞれシックネスゲージで凹凸量を確認する方法もありますが、これは測定というよりも合否判定に近い方法です。この方法では曲がっている方向に注意しなければなりません。定盤に対して凸であるとゲージを指し見込み具合で合否を判断できますが、定盤に対して凹であると安定せずにワークの姿勢によってはどのようなゲージも挿入出来てしまうため正しい判定ができません。またS字形状のワークに対しても同様のため、ある程度形状が推定できているワークに対してのみ有効です。
φありの場合
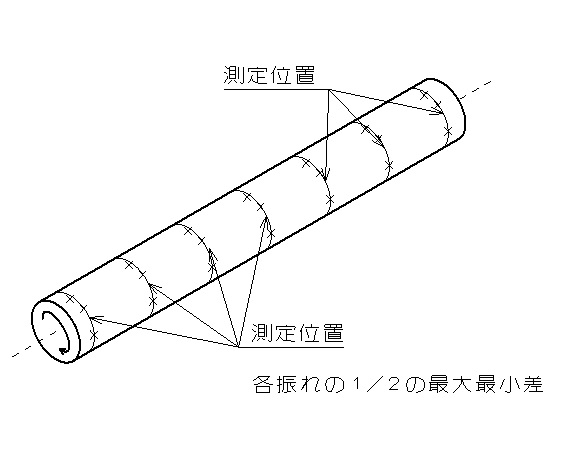
φなしは測定した一軸線上の最大値が真直度となると説明しましたね。しかしφありの場合はある円筒状内の凹凸量を評価するため、それぞれの測定軸線上の凹凸量の相関関係が含まれます。そのためこれまで測定したように軸方向にワークや測定器をスライドするようなやり方では正しい評価ができません。まず測定は両センタのように回転中心が変わらない両持ちになるようにワークを指示します。(Vブロックなどで支持し、ワーク外径を基準に回転させると回転中心が変わるため本測定に使用はできない)その状態で端面から任意の位置で一回転させ、振れ(最大最小差)の1/2を求めます。これを軸方向に移動させ、繰り返します。すべて測定を終えたら、それぞれ求めた値(振れの1/2)の最大最小差が真直度になります。
4.まとめ
・「一方向」「互い平行な二方向」「方向を定めない」に大別される。
・Φなしは評価する線上を独立して評価するが、φありは互いの評価面を相関的に評価する
・真直度は傾きをキャンセルした状態の最大最小差である。
・円筒形状(φなし)はXYの2方向の最大値で評価する
・円筒形状(φあり)は複数個所の1回転の振れの1/2の最大最小差で評価する
以上です。






コメント